- Основні поняття
- Арифметичний квадратний корінь числа
- Таблиця квадратних коренів натуральних чисел від 1 до 100
- Корінь n-го степеня
- Рівняння з квадратним коренем
- Властивості кореня
- Дії з коренями
- Як JustSmart може допомогти підготуватися до НМТ?
Вивчення квадратного кореня починається ще у 8 класі шкільної програми і є невіднятною частиною багатьох математичних задач. Знання властивостей квадратного кореня та вміння його обчислювати є важливими для успішного складання Національного мультипредметного тесту (НМТ), оскільки завдання з цієї теми завжди є на іспиті. Це можуть бути як прості обчислення, так і складніші задачі, що вимагають застосування властивостей коренів.
Окрім цього, квадратні корені є основою для розуміння багатьох інших математичних тем, таких як квадратичні рівняння, геометрія, тригонометрія тощо, онлайн-школи для дітей та підлітків JustSmart допоможе розібратися з цією темою.
Основні поняття
Квадратним коренем із числа а називають число, квадрат якого є числом а.
Видобування квадратного кореня є оберненою дією до піднесення до квадрата.
Важливо! Квадратний корінь з 0 дорівнює 0.
Квадратного кореня з числа менше за 0 не існує, адже нема числа, яке у квадраті давало б від’ємне число.
Онлайн-курси підготовки до НМТ-2026 від JustSmart!
- Онлайн-заняття з досвідченими викладачами.
- Унікальні навчальні матеріали.
- Психологічні тренінги та практичні лайфхаки.
Арифметичний квадратний корінь числа
Арифметичним коренем числа а називають невід’ємне число, квадрат якого дорівнює а.
Арифметичний квадратний корінь позначається знаком √, наприклад, √81=9.
Число 81 має два корені, але додатний з них всього один: 9, він і буде називатися арифметичним квадратним коренем.
Запис √81=9 читають так:: “Квадратний корінь з 81 дорівнює 9”, тобто слово арифметичний зазвичай не вживають.
- Знак √ називають знаком квадратного кореня або радикалом.
- Вираз, що стоїть під знаком радикала, називається підкореневим виразом.
Таблиця квадратних коренів натуральних чисел від 1 до 100
Корінь n-го степеня
Коренем n-го степеня (n=2,3,4,5…) з числа a називається таке число b, n-ий степінь якого дорівнює a:
Корінь парного степеня: визначений тільки для невід’ємних чисел в множині дійсних чисел.
Корінь непарного степеня: визначений для всіх дійсних чисел, як для невід’ємних, так і для від’ємних.
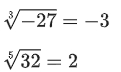
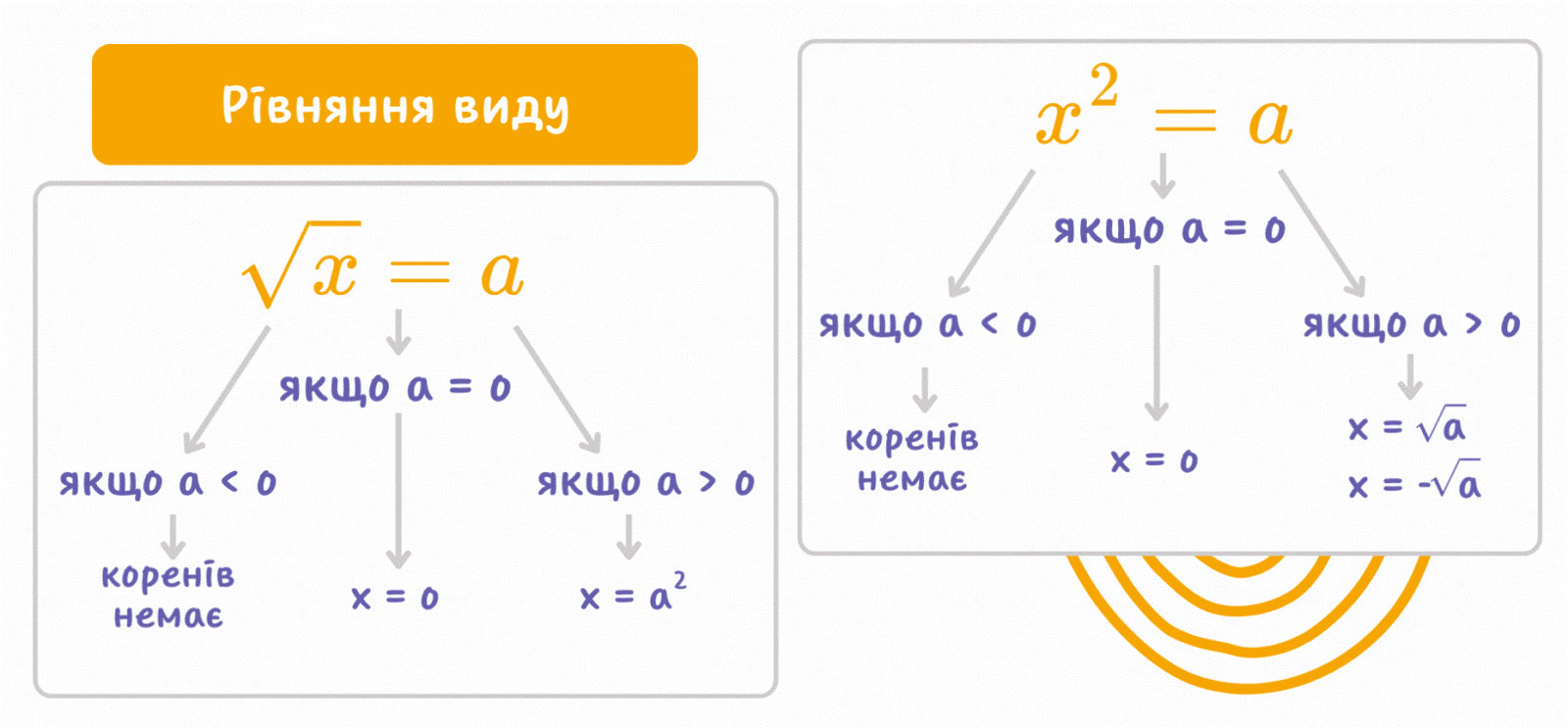
Рівняння з квадратним коренем
Властивості кореня
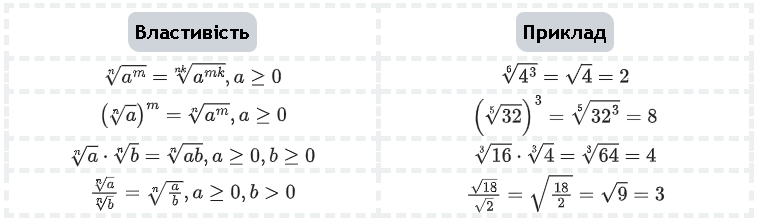
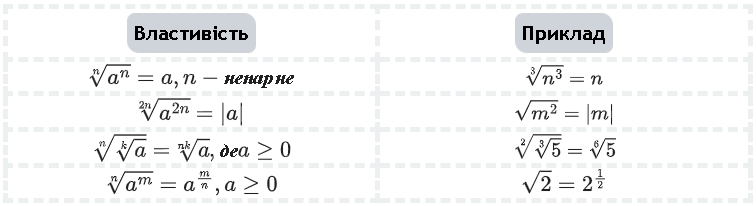
Дії з коренями
Додавання і віднімання кореневих виразів можливе тільки тоді, коли вони мають однаковий підкореневий вираз. Тобто можливо додавати та віднімати
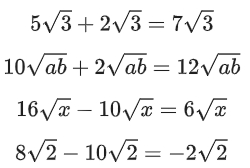
Корені з однаковими підкореневими виразами додаються та віднімаються за тими ж правилами, що і звичайні числа.
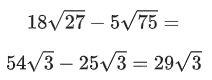
Якщо підкореневі вирази різні, то спочатку треба спростити корені, якщо це можливо, а потім виконувати додавання чи віднімання.
Читайте також: Що таке дійсні числа?
Приклади завдань для самостійного розв’язування
- Обчисліть: √144.
- Знайдіть значення виразу √81+√49.
- Обчисліть значення виразу √64/4.
Як JustSmart може допомогти підготуватися до НМТ?
JustSmart пропонує ефективні курси підготовки до НМТ-2026, на яких:
- Діє гарантія вступу на бюджет: ми гарантуємо вступ на бюджет або повертаємо кошти за навчання.
- Закриваємо всі потреби в підготовці до НМТ:
- Навчальні вебінари.
- Консультації з викладачем.
- Психологічні тренінги.
- Лайфхаки та рекомендації щодо складання НМТ.
З допомогою нашої онлайн-школи ви зрозумієте всі процеси іспиту, напишете якісний мотиваційний лист, будете в курсі всіх новин та нововведень НМТ та отримаєте консультацію щодо питання, куди краще вступати.
Крім підготовки до НМТ, у нас є онлайн-курси математики для учнів з 1-11 класів. Ці курси допоможуть закласти міцний фундамент знань та підготуватися до майбутніх навчальних викликів. Репетитор математики онлайн допоможе пробудити інтерес до предмета. Наші уроки побудовані на діалозі, практиці та чітких поясненнях. Ви забудете про зубріння формул і нарешті зрозумієте, як працює математика. Почніть із пробного заняття!
Також пропонуємо уроки англійської для дітей у JustSchool, які сприятимуть успіху дитини в навчанні, розширюючи можливості для міжнародної комунікації та співпраці.
Читайте також: Усе про дроби та дії з дробами
Отже, знання властивостей квадратного кореня та навички роботи з ним є важливою частиною підготовки до НМТ та успішного складання тесту. Вивчення цієї теми допоможе учням не тільки отримати високі бали на тестуванні, але й краще зрозуміти багато аспектів математики, що трапляються в реальному житті.
*Відповіді та пояснення до завдань
- Обчисліть: √144.
Розв’язання: квадратний корінь з 144 дорівнює такому числу, яке при піднесенні до квадрату дає 144. Це число 12, оскільки 12·12=144. Відповідь: √144=12.
- Знайдіть значення виразу √81+√49.
Розв’язання: Обчислюємо кожний квадратний корінь окремо:
- √81=9, оскільки 9·9=81.
- √49=7, оскільки 7·7=49.
Тепер додаємо ці значення: 9+7=16.
Відповідь: √81+√49=16.
- Обчисліть значення виразу √64/4.
- Спочатку обчислюємо дріб під коренем: 64/4=16.
- Тепер знаходимо квадратний корінь з 16: √16=4, оскільки 4·4=16.
Відповідь: √64/4=4.
