- Властивості та типи розв’язання систем рівнянь
- Найпоширеніші неочевидні помилки у кожному з методів розв’язку систем рівнянь
- Системи з трьома невідомими
- Цікаві факти
Уявіть, що ви – детектив, а кожне рівняння у системі – це окрема підказка. Окремо вони майже нічого не скажуть, але разом відкриють повну картину. Так працюють системи рівнянь.
Вони допомагають розраховувати витрати пального в авто, прогнозувати погоду і навіть знаходити злочинців за сигналом телефону. А у школі ця тема дає змогу швидко й логічно знаходити відповіді на задачі, прогляньмо їх.
Мінізадача 1:
У кінотеатрі продали 100 квитків: дитячі по 80 грн і дорослі по 120 грн. Усього вторгували 10 000 грн. Скільки було кожного виду квитків?
Це класичний приклад, який можна розв’язати за допомогою системи рівнянь.
Мінізадача 2:
Два автобуси виїхали з різних міст одночасно назустріч один одному. Швидкість першого – 60 км/год, другого – на 20 км/год більша. Через 2 години вони зустрілися. Яка відстань між містами?
І знову – система рівнянь допоможе знайти відповідь.
Вивчивши кілька простих методів, ви зможете розв’язувати такі задачі швидше, ніж звариться чайник. І це стане гарним бонусом при онлайн-підготовці до НМТ.
Онлайн-курси підготовки до НМТ-2026 від JustSmart!
- Онлайн-заняття з досвідченими викладачами.
- Унікальні навчальні матеріали.
- Психологічні тренінги та практичні лайфхаки.
💡 Цікавий факт: Перші системи рівнянь з’явилися ще у вавилонських глиняних табличках близько 2000 року до н.е., і використовувалися для розрахунків в торгівлі та будівництві.
Властивості та типи розв’язання систем рівнянь
Система рівнянь – це набір рівнянь, які виконуються одночасно. Іншими словами, ми шукаємо спільний розв’язок: значення змінних, які підходять до кожного рівняння з системи.
Від того, які рівняння входять у систему, вона може бути лінійною або нелінійною. У кожного типу – свої властивості, способи розв’язання та навіть типові помилки учнів.
Системи з двома рівняннями і двома невідомими
Це найпоширеніший тип систем. Маємо два рівняння і дві змінні, наприклад, x і y. Мета – знайти такі пари чисел (x,y), які задовольняють обидва рівняння одночасно.
Приклад:
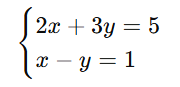
Така система може мати:
- Один розв’язок – коли дві прямі перетинаються в одній точці.
- Безліч розв’язків – коли рівняння описують одну й ту саму пряму.
- Жодного розв’язку – коли прямі паралельні і не перетинаються.
Цей тип систем легко візуалізувати графічно: кожне рівняння – це пряма на площині, а розв’язок – це точка їх перетину.
Системи з трьома рівняннями і трьома невідомими
Тут маємо три рівняння і три змінні, наприклад, x, y, z. Вони описують площини у тривимірному просторі. Знайти розв’язок означає знайти точку, яка лежить одночасно на всіх трьох площинах.
Приклад:
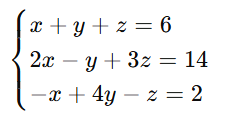
Можливі випадки:
- Один розв’язок – три площини перетинаються в одній точці.
- Безліч розв’язків – площини перетинаються по прямій або лежать на одній площині.
- Жодного розв’язку – площини не мають спільної точки (перетинаються парами, але не всі разом).
Розв’язати таку систему складніше, ніж з двома рівняннями, тому часто використовують методи алгебри, наприклад, метод Крамера або метод підстановки.
Змішані системи (лінійно-нелінійні)
Іноді система містить і лінійні, і нелінійні рівняння. Лінійне рівняння – це таке, в якому змінні стоять в першому степені (без добутків між ними). Нелінійне – коли є змінні у степенях, добутках, або під коренем, наприклад:
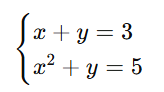
Така система називається змішаною, бо має і лінійне, і нелінійне рівняння. Розв’язувати їх складніше, бо:
- Методи для лінійних систем (підстановка, додавання) не завжди застосовні напряму.
- Потрібно спочатку висловити одну змінну через іншу з лінійного рівняння, а потім підставити у нелінійне.
- Результат може бути кілька розв’язків або взагалі їх відсутність.
Щоб дізнатися більше та системно розвивати свої математичні навички, рекомендуємо приєднатися до курсів математики для дітей JustSmart.
Найпоширеніші неочевидні помилки у кожному з методів розв’язку систем рівнянь
Графічний метод
Неправильне масштабування осей: Якщо вісь x та вісь y мають різні масштаби, то кут нахилу прямих на графіку буде викривлено, і точка перетину може виглядати зовсім інакше, ніж у реальності.
Ігнорування округлень: Навіть невеликі похибки в побудові графіка (через неточний малюнок або заокруглення координат) можуть спричинити неправильне визначення кількості або точного розташування розв’язків.
Неправильний вибір типу графіка для нелінійних рівнянь: Якщо система має хоча б одне нелінійне рівняння (парабола, гіпербола), неправильне розуміння форми кривої призведе до помилки у визначенні точок перетину.
💡 Практичні завдання на графічний метод можна знайти у тестах НМТ з математики, де зібрані найактуальніші завдання для підготовки.
Метод підстановки
Вибір «важкої» змінної для підстановки: Якщо виражати складний вираз (наприклад, дробовий, містить корінь або степінь), подальші обчислення значно ускладнюються і зростає ймовірність помилок.
Пропуск дужок при підстановці: Наприклад, підставити x=2−y у 3x як 3⋅2−y замість 3⋅2−3y – класична помилка, що змінює весь результат.
Ігнорування обмежень на змінні: При нелінійних системах або при розв’язанні через підстановку можуть з’явитися розв’язки, які не задовольняють початкові умови (наприклад, негативні значення там, де їх бути не може). Цього іноді не помічають.
Метод додавання (виключення)
Неправильне домноження рівнянь: Домноження рівнянь на коефіцієнти без перевірки знаків може призвести до того, що замість виключення змінної ви додасте два однакові за знаком коефіцієнти, а не протилежні.
Змішування коефіцієнтів: Помилка при копіюванні коефіцієнтів призведе до хибних результатів, але її легко пропустити, якщо не перевіряти кроки.
Ігнорування особливих випадків: Наприклад, якщо після додавання вийшло рівняння 0=0 – це означає безліч розв’язків, а не відсутність. А якщо вийшло 0=c, де c≠0 – система несумісна. Помилки трапляються, коли ці випадки не розпізнають.
Загальні помилки для всіх методів
- Не перевіряють знайдений розв’язок в обох рівняннях. Особливо критично для складних систем, де один рівень розв’язку може бути правильним, а другий – ні.
Втрата або додавання знаку мінус при перенесенні членів. Помилки зі знаками – найбільш часта причина неправильних відповідей. - Забування про множення на нуль при виключенні змінної (наприклад, ділення на змінну, яка може дорівнювати нулю). Це може призвести до втрати розв’язків або до появи помилкових.
- Ігнорування домену змінних (наприклад, цілі, додатні числа, числа з певними обмеженнями), що може давати «математично правильні», але неприйнятні розв’язки для задачі.
Системи з трьома невідомими
Приклад 1. Розв’язання методом підстановки для системи з трьома невідомими
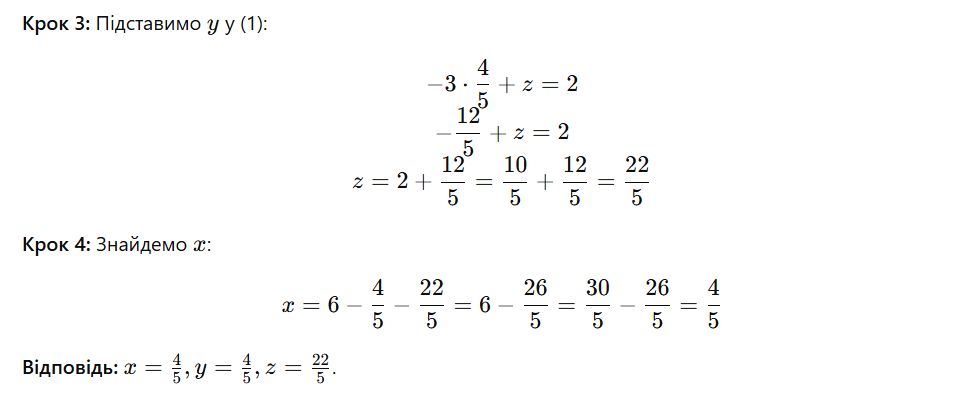
Приклад 2. Розв’язання методом додавання для системи з трьома невідомими
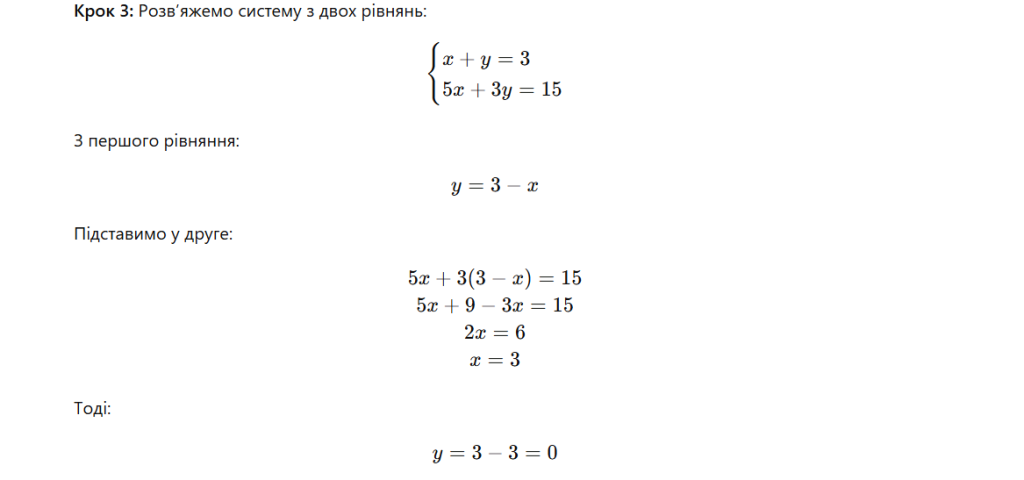
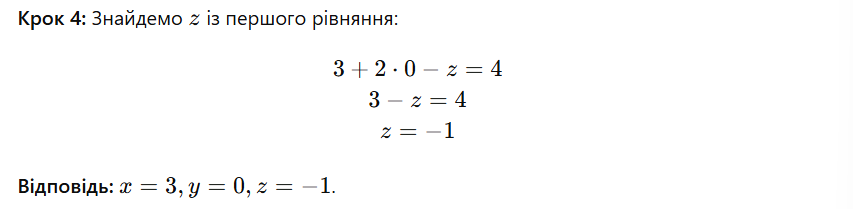
Цікаві факти
Найкращі результати досягаються, коли учень не просто знає формули, а розуміє логіку і принципи розв’язання різних типів систем, володіє кількома методами і вміє вибирати найефективніший.
Одне з найвідоміших історичних досліджень систем рівнянь пов’язане з іменем французького математика XVII століття Рене Декарта. Саме він уперше систематизував методи розв’язання систем лінійних рівнянь у своїй праці «Геометрія» (1637 р.), де показав, як алгебра та геометрія взаємопов’язані через координатний метод. Цей прорив поклав початок сучасному аналітичному способу розв’язання систем рівнянь і відкрив нові можливості для розвитку математики, фізики та інженерії.
Вивчення математики часто пов’язане з розвитком логічного мислення, яке також покращує здатність до вивчення іноземних мов. Наприклад, заняття з англійської мови для дітей і підлітків сприяють розвитку аналітичних навичок, що корисно і при розв’язанні математичних задач. Для тих, хто хоче поєднати якісну підготовку з математики та вивчення англійської, існують спеціальні курси, наприклад, у JustSchool – англійська для дітей та підлітків.
