- Анатомія фігури та золотий закон Піфагора
- Ідентифікація сторін та властивості кутів
- Фундаментальні формули та код Піфагора
- Спеціальні випадки та магія пропорцій
- Приховані закони: геометричне середнє та подібність
- Перевір свою майстерність з підказками
- Висновки про прямокутний трикутник
Розберемо, що таке прямокутний трикутник та які в нього є властивості. Читай статтю й легко опануй основи геометрії!
Починаючи від вимірювання земельних ділянок тисячоліття тому до сучасних інженерних розрахунків, які забезпечують точність лазерних систем, світом керує незмінний геометричний ідеал: прямокутний трикутник. Ця фігура виступає як універсальний інструмент, що гарантує точність і гармонію в усіх прикладних галузях.
Ми пропонуємо поглянути на цю геометричну форму як на фундамент прикладної математики, розкриваючи її приховані секрети, потужний потенціал та елегантні закони. Наша мета — перетворити прямокутний трикутник та його властивості з об’єкта зазубрювання на набір інструментів, що допоможуть вам домінувати над геометричними задачами та впевнено почуватися на будь-якому тестуванні.
Онлайн-курси підготовки до НМТ-2026 від JustSmart!
- Онлайн-заняття з досвідченими викладачами.
- Унікальні навчальні матеріали.
- Психологічні тренінги та практичні лайфхаки.
Анатомія фігури та золотий закон Піфагора
Задовго до того, як теорема була формально записана, її вже активно використовували. У Стародавньому Єгипті існувала каста “гарпедонаптів” — вимірювачів землі, які використовували мотузку, поділену вузлами на 12 рівних частин, щоб після розливу Нілу швидко відновити межі ділянок. Розтягуючи мотузку в трикутник зі сторонами 3, 4 і 5 одиниць, вони отримували ідеально прямий кут. Це стало першим прикладним доказом того, що прямокутний трикутник є ключем до точності.
Ідентифікація сторін та властивості кутів
Унікальність прямокутного трикутника криється в його головній ознаці — нерухомому куті в 90 градусів, що накладає особливі вимоги на термінологію та внутрішні зв’язки. Саме цей прямий кут виділяє цю фігуру і диктує унікальну термінологію для її сторін:
- Катети прямокутного трикутника: Дві сторони, які формують прямий кут.
- Гіпотенуза прямокутного трикутника: Завжди найдовша сторона, розташована навпроти прямого кута.
Після того як ми чітко ідентифікували «учасників» цієї геометричної драми — катети та гіпотенузу — логічно перейти до закону, який зв’язує їх усіх воєдино, до найвеличнішого досягнення античної математики.
Якщо ви відчуваєте, що базові поняття геометрії даються вам або вашій дитині із зусиллями, це легко виправити. Освоїти логіку та навчитися мислити геометрично допоможуть наші онлайн-курси математики, розроблені для справжнього розуміння, а не лише для зазубрювання.
Фундаментальні формули та код Піфагора
Серцем усіх прямокутний трикутник формули є, безумовно, Теорема Піфагора, яка встановлює нерозривний зв’язок між довжинами сторін:
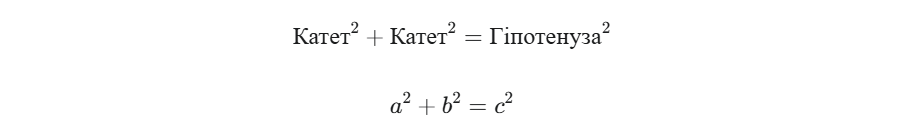
Справжній “хак” криється у використанні Піфагорових трійок — наборів із трьох цілих чисел (a, b, c), які ідеально задовольняють рівняння Піфагора. Знаючи ці трійки, ви можете знайти третю сторону за частки секунди, уникнувши обчислення кореня:
Крім того, важливо пам’ятати формулу для площі, яка значно спрощується:
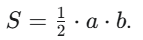
Згідно зі звітом УЦОЯО, у 2024 році 12,8% учасників НМТ не змогли подолати пороговий бал з математики. Це свідчить про необхідність якісної підготовки. Якщо ви прагнете потрапити на бюджет і математика — один із ваших ключових предметів, то вже зараз варто почати курси підготовки до НМТ, щоб почуватися впевнено на іспиті.
Спеціальні випадки та магія пропорцій
Засвоївши головний закон, ми можемо дослідити спеціальні випадки, які перетворюють прямокутний трикутник на справжній математичний «лайфхак» та дозволяють робити складні висновки, лише поглянувши на кути.
Особливі Геометричні “Ключі” та Походження Правила 30 градусів
У світі геометрії однією з найпотужніших властивостей прямокутного трикутника є правило прямокутний трикутник 30 градусів. Його властивість: катет, що лежить навпроти кута 30 градусів, завжди дорівнює половині гіпотенузи.
Як утворилась ця формула?
Щоб утворилась ця формула, достатньо уявити симетричне відображення нашого трикутника вздовж катета, прилеглого до кута 30 градусів. У результаті ми отримаємо рівносторонній трикутник, у якого всі сторони рівні, а всі кути дорівнюють по 60 градусів. Катет початкового трикутника є висотою цієї нової фігури й ділить протилежну сторону навпіл, звідси й випливає дане відношення.
Також не можна забувати про рівнобедрений прямокутний трикутник, у якого катети рівні, а гострі кути — по 45 градусів.
Для доведення ідентичності двох фігур використовуються ознаки рівності прямокутних трикутників, які є спрощенням загальних правил: за гіпотенузою і катетом, або за гіпотенузою і гострим кутом.
Перед тим як перейти до найскладнішого матеріалу, перевірте свої знання основ. Чи готові ви? Пройдіть тести НМТ з математики та точно знатимете свої слабкі місця.
Приховані закони: геометричне середнє та подібність
Справжня інженерна елегантність прямокутного трикутника розкривається, коли ми проводимо висоту до гіпотенузи. Ця дія створює три подібні фігури, об’єднані принципом геометричного середнього (середнього пропорційного):
Ці формули дозволяють обхитрувати розв’язання, оскільки ви можете знайти висоту (яка в іншому випадку вимагала б площі та гіпотенузи), використовуючи лише проєкції. Розуміння цих пропорційних зв’язків — це той рівень, який відрізняє справжнього майстра геометрії.
Освіта не має обмежуватися лише математикою. Комплексний розвиток — це ключ до успіху в сучасному світі. Радимо звернути увагу на курси англійської для дітей в JustSchool та дати своїй дитині додаткову перевагу.
Перевір свою майстерність з підказками
Пропонуємо дві задачі, які перевірять ваше володіння ключовими “хаками”.
Висновки про прямокутний трикутник
Прямокутний трикутник, цей ідеальний геометричний модуль, слугує не просто розділом геометрії, а й ключем до розуміння всієї прикладної математики. Ми побачили, що за основними визначеннями приховані справжні скарби: від єгипетської легенди про вимірювачів землі до законів середнього пропорційного, які дозволяють “обхитрувати” складні розрахунки. Впевнене володіння його властивостями гарантує успіх на іспитах та здатність бачити математичну логіку в навколишньому світі.
Для швидкого повторення та закріплення матеріалу, використовуйте цю таблицю, що охоплює найважливіші закони прямокутний трикутник формули:
