- Історія виникнення паралелограма
- Властивості паралелограма
- Ознаки паралелограма
- Види паралелограма
- Формули паралелограма: як знайти площу та периметр?
- Завдання для самостійного розвитку
- Як JustSmart допоможе легко вивчити паралелограм
- Паралелограм у житті та навчанні
Від бджолиних стільників до архітектурних шедеврів, геометричні фігури оточують нас усюди. Однією з таких фундаментальних і водночас універсальних фігур є паралелограм.
Для багатьох школярів та їхніх батьків ця тема може здатися складною, але насправді паралелограм – це проста і логічна фігура. Детально розберімося, що таке паралелограм, які в нього є секрети, звідки він взявся і чому він такий важливий.
Онлайн-курси підготовки до НМТ-2026 від JustSmart!
- Онлайн-заняття з досвідченими викладачами.
- Унікальні навчальні матеріали.
- Психологічні тренінги та практичні лайфхаки.

Історія виникнення паралелограма
Поняття паралелограма сягає глибокої давнини. Сам термін походить від давньогрецьких слів parallelos — «паралельний» і gramma — «лінія».
Цю фігуру описав понад дві тисячі років тому давньогрецький математик Евклід у своїй праці «Начала». Він визначив паралелограм як чотирикутник, у якого протилежні сторони паралельні, та довів низку властивостей, якими ми користуємося й сьогодні.
Він не лише дав визначення, але й довів ключові теореми, які ми вивчаємо й досі: наприклад, що діагональ ділить паралелограм на два рівні трикутники, і що у паралелограма протилежні сторони та кути рівні. Саме через дослідження властивостей паралелограма Евклід довів одну з найвідоміших у світі теорем — теорему Піфагора.
Читайте також: Чотирикутники: види, властивості та формули
Властивості паралелограма
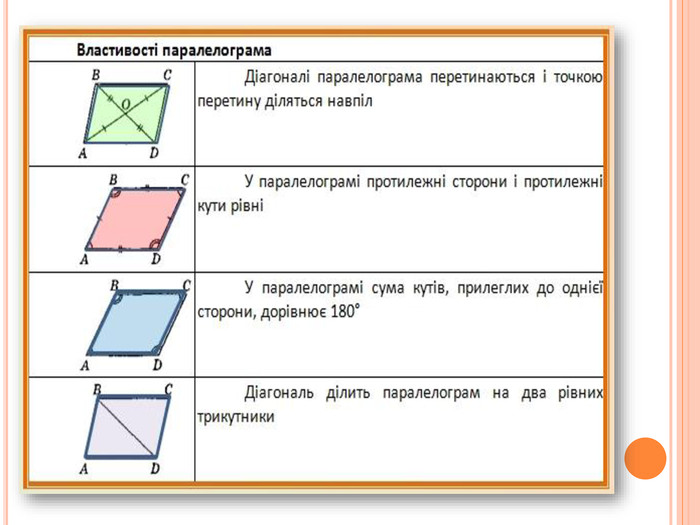
Щоб фігура могла гордо називатися паралелограмом, вона повинна мати певні характеристики. Основні властивості паралелограма допомагають легко його впізнати та розв’язувати задачі.
Властивість 1
Протилежні сторони паралелограми попарно рівні.
Чому? Це легко довести, розглянувши два трикутники, на які діагональ ділить паралелограм. Вони рівні за стороною та двома прилеглими кутами (як внутрішні різносторонні кути при паралельних прямих).
Властивість 2
Протилежні кути попарно рівні.
Властивість 3
Сума кутів паралелограма, прилеглих до однієї сторони, завжди дорівнює 180°.
Чому? Це випливає з властивості внутрішніх односторонніх кутів при паралельних прямих та січній.
Властивість 4
Діагоналі паралелограма точкою перетину діляться навпіл.
Властивість 5
Кожна діагональ ділить паралелограм на два рівних трикутники.
Властивість 6 (Тотожність паралелограма):
Сума квадратів діагоналей дорівнює сумі квадратів усіх його сторін.
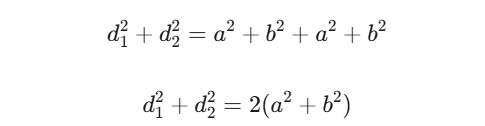
Ознаки паралелограма
А як довести, що перед нами саме паралелограм, а не довільний чотирикутник? Для цього існують ознаки паралелограма. Це, по суті, “зворотні” правила.
Чотирикутник є паралелограмом, якщо виконується хоча б одна з цих умов:
- Якщо у чотирикутника дві протилежні сторони паралельні й рівні.
- Якщо у чотирикутника протилежні сторони попарно рівні.
- Якщо у чотирикутника протилежні кути попарно рівні.
- Якщо у чотирикутника діагоналі перетинаються і точкою перетину діляться навпіл.
Якщо ви помітили хоча б одну з цих ознак – будьте певні, перед вами паралелограм!
Читайте також: Основні геометричні фігури на площині та геометричні величини
Види паралелограма
Паралелограм – це “батько” для цілого сімейства фігур. Деякі з них нам дуже добре знайомі. Основні види паралелограма – це прямокутник, ромб і квадрат. Для кращого засвоєння матеріалу ми зібрали їх характеристики у таблицю.
| Вид | Визначення | Властивості сторін | Властивості кутів | Властивості діагоналей |
| Ромбоїд | “Загальний” паралелограм | Не рівні. | Не дорівнюють 90°. | Діляться навпіл. |
| Прямокутник | Паралелограм, у якого всі кути прямі. | Протилежні рівні. | Всі 90°. | Рівні між собою та діляться навпіл. |
| Ромб | Паралелограм, у якого всі сторони рівні. | Всі рівні. | Протилежні рівні. | Взаємно перпендикулярні та ділять кути навпіл. |
| Квадрат | Паралелограм, у якого всі сторони рівні та всі кути прямі. | Всі рівні. | Всі 90°. | Рівні, взаємно перпендикулярні, ділять кути навпіл. |
Таким чином, квадрат – це одночасно і ромб, і прямокутник, і, звичайно, паралелограм. Він поєднує в собі властивості їх усіх.
Формули паралелограма: як знайти площу та периметр?
Жодна геометрична фігура не обходиться без формул. Для паралелограма ключовими є формула паралелограма для периметра та площі. Також на малюнку наведено деякі площі наслідкових фігур.

Також, якщо ви знаєте сторони a, b і одну діагональ d1, ви можете знайти площу. Діагональ ділить паралелограм на два рівних трикутники зі сторонами a, b, d1. Площу такого трикутника можна знайти за формулою Герона, а потім помножити на 2.
Завдання для самостійного розвитку
Теорія найкраще засвоюється на практиці. Спробуйте розв’язати кілька завдань, щоб закріпити матеріал:
- Задача (Властивості): Одна зі сторін паралелограма 12 см, інша на 5 см коротша. Знайдіть периметр паралелограма.
- Задача (Кути): Сума двох кутів паралелограма дорівнює 240°. Знайдіть усі кути фігури. (Підказка: чи можуть це бути кути, прилеглі до однієї сторони?)
- Задача (Площа): Сторони паралелограма 6 см і 10 см, а кут між ними 150°. Знайдіть площу паралелограма.
- Задача (Просунута): Діагоналі паралелограма дорівнюють 10 см і 14 см, а одна зі сторін – 9 см. Знайдіть іншу сторону. (Підказка: використайте тотожність паралелограма).
Також радимо пройти пробні тести НМТ з математики онлайн, аби потренуватися на форматі, наближеному до реального іспиту.
Як JustSmart допоможе легко вивчити паралелограм
Паралелограм — це одна з базових тем шкільної геометрії, але зрозуміти всі його властивості, формули та ознаки самостійно буває непросто. Саме тому команда JustSmart створила сучасні освітні програми, які допомагають учням не просто зазубрити матеріал, а його зрозуміти.
- На курсах математики для дітей учні крок за кроком вивчають геометричні фігури, розбираються у формулах площ і периметрів, вчаться застосовувати знання на практиці.
- Під час онлайн-підготовки до НМТ викладачі JustSmart пояснюють, як розв’язувати задачі на паралелограм, типові для НМТ з математики — з детальними прикладами та покроковими розв’язуваннями.
- А щоб розвивати логіку, пам’ять і мислення в цілому, радимо спробувати курси англійської для дітей та підлітків в JustSchool — це допоможе розвивати мовлення та навички критичного мислення, необхідні навіть для розуміння складних математичних понять.
У JustSmart навчання перетворюється на цікаву подорож, де кожна тема — від паралелограма до тригонометрії — стає простою, зрозумілою й корисною для майбутніх успіхів.
Паралелограм у житті та навчанні
Паралелограм — не просто абстрактна фігура з підручника. Він трапляється в архітектурі, дизайні, техніці та природі.
- У природі: форма крил метеликів і навіть малюнки на панцирах черепах мають риси паралелограма.
- В архітектурі: вікна, фасади, сходи й навіть мости часто побудовані на принципі паралелограмів, щоб забезпечити міцність конструкції.
- У техніці: у підйомних механізмах застосовують паралелограмні важелі — саме вони дозволяють утримувати рівновагу і плавність руху.
- У дизайні: логотипи, орнаменти, елементи шрифту часто використовують форму паралелограма для створення динамічності та гармонії.
Знання властивостей паралелограма допомагає не лише у розв’язуванні задач НМТ, але й у розумінні реального світу.
Паралелограм – це не просто чотирикутник, а одна з наріжних фігур у світі геометрії. Розуміння його властивостей, ознак та видів (прямокутника, ромба, квадрата) відкриває двері до вирішення складніших завдань у математиці, фізиці та інженерії.
Головне – пам’ятати, що його сила у паралельності та рівності протилежних сторін. А з правильними інструментами для навчання, будь-яка складна тема стає простою та захопливою.

 Усі статті
Усі статті Для підлітків
Для підлітків Підготовка до НМТ
Підготовка до НМТ Статті про Roblox
Статті про Roblox Уроки математики
Уроки математики
 АвторШабанова Анастасія
АвторШабанова Анастасія 





