- Історичний екскурс: від Єгипту до сучасності
- Найпростіші геометричні фігури на площині
- Геометрія та інші науки
Геометрія — це не просто набір понять і фігур. Це ключ до розуміння простору — навколишнього та внутрішнього. Вона навчає нас мислити візуально, аналітично і логічно.
Тема «Основні геометричні фігури на площині та геометричні величини» — це старт до світу просторового мислення: від точок і відрізків до площі, кута й формул. Цей фундаментальний розділ формує просторову уяву, аналітичні стратегії та вміння розв’язувати задачі, що стануть у пригоді у фізиці, інженерії, архітектурі, інформатиці, природознавстві та мистецтві.
Статистика підтверджує: просторові здібності мають вагоме значення для навчальних успіхів. Дослідження показують, що просторове мислення пояснює від 8,8% до 22,6% варіації у математичних результатах учнів (https://www.sciencedirect.com/). А інтервенційне навчання, спрямоване на розвиток просторових навичок, веде до помітних покращень у геометрії — як показало дослідження серед одинадцятикласників, де навчання за методикою ELPSA зміцнило саме результати з геометричних задач (SpringerLink).
Геометрія також має реальні соціально-економічні наслідки. За даними Федерального резервного банку Клівленда, випускники, які успішно завершили курс геометрії (на відміну від тих, хто не пройшов його), мають на 13% вищу середню погодинну ставку ($14,36 проти $12,70) і дещо нижчий рівень безробіття (27% проти 33%) (Cleveland Fed).
У трудовій сфері теж є сильна кореляція: 29% фахівців у ремісничих і технічних професіях використовують геометрію та тригонометрію щодня; причому практично 94% усіх працівників якоюсь мірою використовують математику (The Mathematics Society). А серед професій, де геометрія є ключовою — архітектори, міські планувальники, аналітики географічних інформаційних систем (GIS)
Історичний екскурс: від Єгипту до сучасності
Геометрія бере свій початок у Давньому Єгипті, де після розливів Нілу землеміри вимірювали площі полів і відновлювали межі ділянок, закладаючи перші практичні основи просторового мислення. У Давній Греції ці знання перетворилися на науку: Евклід у праці «Начала» систематизував аксіоми й теореми, заклавши логіку доказів, тоді як Піфагор відкрив фундаментальний зв’язок між сторонами прямокутного трикутника, а Архімед досліджував площі й об’єми, розробляючи методи наближених обчислень числа π.
Сьогодні геометрія застосовується не лише для креслення чи інженерних розрахунків, а й лежить в основі комп’ютерної графіки, проєктування мостів, робототехніки, аналізу ДНК та віртуальної реальності, демонструючи безперервний зв’язок між теоретичними принципами і практичними потребами людства.
Найпростіші геометричні фігури на площині
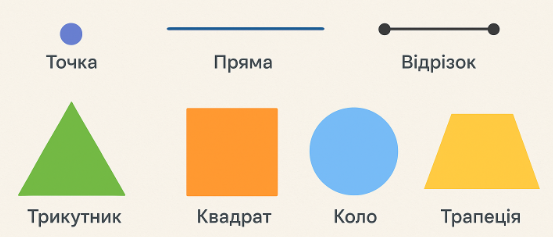
Геометрія починається з точки — найменшого елемента, що не має довжини, ширини чи висоти, але позначає певне положення на площині. Можна уявити її як місце на карті, де знаходиться скарб або центр об’єкта. Саме з точки починаються всі подальші побудови: лінії, промені та багатокутники.
Якщо з’єднати дві точки, ми отримаємо відрізок — лінію з визначеним початком і кінцем, яка вимірює відстань між цими точками. Відрізки формують сторони трикутників, квадратів і прямокутників. Якщо ж лінія простягається нескінченно в обидва боки, виникає пряма, яка задає напрямок, а промінь — це лінія з початком у певній точці, що простягається лише в один бік, подібно до сонячного променя.
Коли два промені виходять з однієї точки, утворюється кут, який показує відхилення одного променя від іншого. Кути використовуються для побудови багатокутників і визначення нахилів, наприклад, у дахах будинків або в каркасах мостів.
Серед багатокутників основними є трикутник, квадрат, прямокутник, ромб і трапеція. Трикутник, маючи три сторони і три кути, є найміцнішою формою для конструкцій, бо не змінює форму під тиском. Квадрат та прямокутник зустрічаються в повсякденному житті — у вікнах, дверях і книжках. Ромб і трапеція допомагають створювати більш складні форми та декоративні елементи.
Особливе місце займають коло та круг. Коло — це множина точок, що знаходяться на однаковій відстані від центру, а круг — це площина всередині кола. Вони зустрічаються в колесах, годинниках, планетах і навіть в дизайні сучасних гаджетів. Кола і круги допомагають описувати об’єкти, що обертаються, і формувати симетричні конструкції.
Хоча всі ці фігури здаються простими, вони є основою всієї геометрії, адже будь-яка складна фігура, креслення чи тривимірна модель починаються саме з точки, лінії, кута або простого багатокутника.
Для тих, хто бажає поглибити свої знання та підготуватися до майбутніх іспитів, корисною буде онлайн-підготовка до НМТ, а для дітей, які хочуть систематично покращувати математичні навички, варто звернути увагу на онлайн курси математики, де складні теми подаються доступно та інтерактивно.
Основні геометричні фігури на площині та їх геометричні величини
Кожна геометрична фігура має певні властивості, які можна виміряти та обчислити за допомогою геометричних величин. Найважливіші з них — довжина, площа та кут.
- Довжина — це розмір відрізка або сторони фігури, що дозволяє вимірювати периметр. Наприклад, для прямокутника довжина і ширина визначають його розмір, а сума сторін дає периметр.
- Площа показує, яку площу займає фігура на площині, і вимірюється в квадратних одиницях (см², м²). Наприклад, площа квадрата обчислюється як квадрат його сторони, а площа трикутника — як половина добутку сторони на висоту.
- Кут описує відхилення одного променя від іншого та вимірюється у градусах або радіанах. Кути формують трикутники, чотирикутники і складніші багатокутники.
Для зручності навчання та швидкого запам’ятовування можна скласти таблицю, що поєднує фігуру, її величини, формули та приклади:
| Фігура | Основні величини | Формули | Приклади використання |
| Трикутник | Сторони, периметр, площа, кути | P = a + b + c S = ½·a·h | Каркас даху, трикутні ферми |
| Квадрат | Сторона, периметр, площа | P = 4a S = a² | Плитка, книжка, дошка |
| Прямокутник | Сторони, периметр, площа | P = 2(a + b) S = a·b | Вікна, двері, рамки |
| Ромб | Сторона, діагоналі, периметр, площа | P = 4a S = ½·d₁·d₂ | Декор, візерунки |
| Трапеція | Основа, сторони, висота, периметр, площа | P = a+b+c+d S = ½·(a+b)·h | Декор, архітектурні елементи |
| Коло | Радіус, діаметр, довжина кола, площа | L = 2πr S = πr² | Колеса, годинники, круглі столи |
Задачі з підрахунком
Задача 1. Знайти площу прямокутної кімнати розмірами 4,5 м × 3,2 м.
Розв’язання: S = 4,5 × 3,2 = 14,4 м².
Відповідь: 14,4 м².
Задача 2. Обчислити довжину кола з діаметром 12 см.
C = πd = 3,14 × 12 = 37,68 см.
Відповідь: ≈ 37,7 см.
Задача 3. Знайти кількість фарби, потрібної для фарбування круглого басейну діаметром 8 м, якщо на 1 м² витрачається 0,25 л фарби.
S = πr² = 3,14 × 4² = 50,24 м². Фарба: 50,24 × 0,25 = 12,56 л.
Відповідь: ≈ 12,6 л.
Задачі на доведення
Задача 4. Довести, що діагоналі квадрата рівні та перетинаються під прямим кутом.
Доведення:
У квадраті всі сторони рівні, а всі кути прямі (90°). Проведемо діагоналі — вони з’єднують протилежні вершини квадрата. Кожна діагональ ділить квадрат на два рівнобедрені прямокутні трикутники, у яких сторони квадрата є катетами, а діагональ — гіпотенузою.
За теоремою Піфагора довжини обох діагоналей однакові:
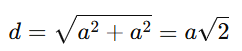
де a — довжина сторони квадрата.
Крім того, у точці перетину діагоналі ділять одна одну навпіл і утворюють чотири рівні прямокутні трикутники, тому діагоналі перетинаються під прямим кутом (90°).
Висновок: діагоналі квадрата завжди рівні та перетинаються під прямим кутом.
Задача 5. Довести, що сума внутрішніх кутів трикутника дорівнює 180°.
Доведення:
Розглянемо трикутник ABC. Через вершину A проведемо пряму, паралельну основі BC. Позначимо кути, що утворилися при перетині цієї прямої з сторонами трикутника.
За властивістю паралельних прямих:
- кут при вершині B рівний куту при вершині A, що лежить на прямій;
- кут при вершині C рівний іншому куту при A.
Таким чином, сума трьох внутрішніх кутів трикутника дорівнює сумі трьох кутів при прямій (тобто 180°).
Висновок: у будь-якому трикутнику сума внутрішніх кутів завжди дорівнює 180°.
💡 Порада: для тренування складніших задач і підготовки до НМТ/ЗНО з математики можна використовувати тести НМТ з математики. Регулярне тренування допомагає швидко опановувати різні типи завдань і розвивати логічне мислення.
Як уникнути неочевидних помилок у геометричних задачах
Часто учні вважають, що головне — швидко підставити числа у формули, і саме ця спокуса призводить до найпоширеніших помилок. Наприклад, можна переплутати довжину сторони і радіус кола, забути перевести одиниці або неправильно визначити, яку величину потрібно шукати. Проблема не в обчисленнях, а в недостатньому аналізі задачі на початковому етапі.
Щоб уникнути цього, важливо застосовувати системний підхід, який тренує логіку та уважність:
- Чітко виділіть дані: запишіть усі відомі величини та умови. Не просто перепишіть числа, а підкресліть, що це — сторона, радіус, висота, кут тощо. Так ви зразу помітите, якщо чогось не вистачає.
- Формулюйте мету: визначте, що саме потрібно знайти. Не перескакуйте одразу до обчислень — розуміння кінцевої мети допомагає обирати правильні формули і послідовність кроків.
- Обміркуйте послідовність дій і формули: подумайте, які формули застосовуються, і які величини потрібно поєднати. Можна навіть намалювати схему або зробити коротку «підказку на папері» для кожного кроку.
Ця стратегія допомагає побачити приховані підводні камені, наприклад відсутні дані, неправильні одиниці або зайві обчислення. Навіть складніші задачі, які здаються заплутаними, на перший погляд, стають контрольованими і зрозумілими.
Геометрія та інші науки
Геометрія пронизує майже всі сфери нашого життя, демонструючи, як математичні форми допомагають описувати, моделювати і створювати навколишній світ.
Фізика: планети рухаються по еліпсах, як це описав Йоганн Кеплер, а хвилі, від звукових до електромагнітних, зручно зображати синусоїдою. Дзеркала та інші оптичні прилади працюють завдяки закону відбиття, де кут падіння дорівнює куту відбиття, що дозволяє точно передавати світлові промені.
Архітектура: від величних пірамід Єгипту до готичних соборів і сучасних хмарочосів — усі ці споруди побудовані на основі геометричних форм. Використання «золотого перетину» допомагає створювати гармонійні пропорції та естетично привабливі конструкції, що зачаровують око.
Інформатика: сучасні комп’ютерні ігри, анімація та 3D-моделі будуються з багатокутників, а алгоритми 3D-моделювання застосовують геометричні формули для обчислення площ, об’ємів і кутів. Без геометрії неможливі ні віртуальні світи, ні реалістичні графічні ефекти.
Мистецтво: Леонардо да Вінчі та інші майстри епохи Відродження активно використовували геометрію для побудови перспективи та пропорцій у картинах, що робило композиції більш реалістичними і гармонійними. Лінійна перспектива та симетрія — це прямий приклад того, як математика допомагає мистецтву.
Біологія: природа теж знає геометрію. Бджолині стільники мають форму шестикутників, що дозволяє оптимально заповнити площину, використовуючи мінімум воску, а форма клітин організмів часто підпорядкована геометричним закономірностям, які забезпечують ефективність функцій.
Геометрія не лише пояснює світ навколо нас, а й допомагає розвивати логіку та просторове мислення, що важливо для навчання та творчості. Для дітей та підлітків, які хочуть одночасно вдосконалювати свої логічні навички та англійську, існують курси англійської для дітей та підлітків в JustSchool, де навчання проходить цікаво та ефективно.
Вивчення основних геометричних фігур на площині та відповідних величин становить фундамент для системного розуміння просторових структур і математичного аналізу. Засвоєння властивостей точок, прямих, відрізків, кутів та багатокутників дозволяє формалізовано описувати взаємне розташування об’єктів, визначати довжини, площі та кути, а також застосовувати ці знання в розв’язанні практичних і теоретичних задач.
Опанування площинної геометрії створює необхідну базу для переходу до геометрії об’ємних тіл, де додається третій вимір і виникають поняття об’єму, площі поверхні та просторової симетрії.

 Усі статті
Усі статті Для підлітків
Для підлітків Підготовка до НМТ
Підготовка до НМТ Статті про Roblox
Статті про Roblox Уроки математики
Уроки математики
 АвторШабанова Анастасія
АвторШабанова Анастасія 





