- Фундаментальні властивості та закони
- Класифікація чотирикутників
- Обчислення площі чотирикутника
- Вписані та описані чотирикутники
- Висновок
Якщо трикутник є символом абсолютної жорсткості та рівноваги, то чотирикутник є символом універсальності та функціональності. Ця фігура з чотирма вершинами та чотирма сторонами становить основу більшості об’єктів, створених людиною, від планування земельних ділянок до сучасних архітектурних рішень.
Онлайн-курси підготовки до НМТ-2026 від JustSmart!
- Онлайн-заняття з досвідченими викладачами.
- Унікальні навчальні матеріали.
- Психологічні тренінги та практичні лайфхаки.
Чотирикутник визначається як багатокутник, що складається з чотирьох точок (вершин) та чотирьох відрізків (сторін), які їх послідовно з’єднують, за умови, що жодні три вершини не лежать на одній прямій. Розуміння його внутрішньої «логіки» — це ключ до опанування об’ємної геометрії та розв’язання складних завдань.
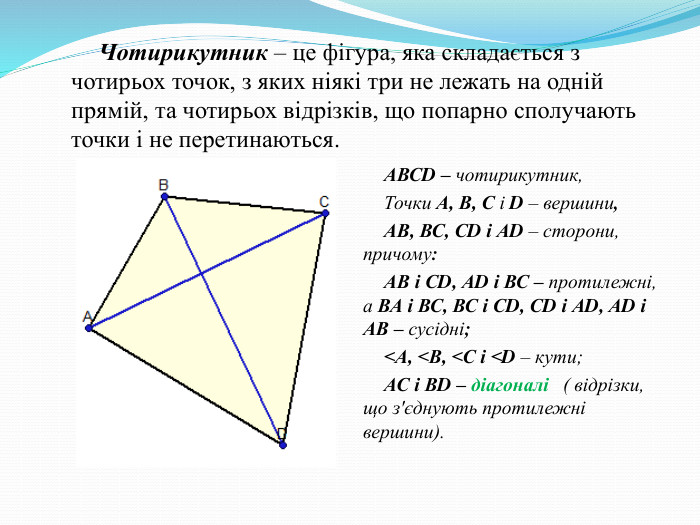
Фундаментальні властивості та закони
Вивчення чотирикутника починається з його незмінних законів.
Закон Інваріантності: Чому 360 градусів?
Ключова константа, що визначає внутрішній простір фігури, – це сума кутів чотирикутника. Вона завжди дорівнює 360 градусів. Ця інваріантність пояснюється елементарним чином: провівши одну діагональ, ми розбиваємо чотирикутник на два трикутники, сума кутів яких становить 180 градусів кожен, що у сумі дає 360.
Лінійна Межа: Периметр чотирикутника
Периметр чотирикутника (P) є його лінійним виміром і обчислюється як проста сума довжин усіх чотирьох сторін (a, b, c, d): P = a + b + c + d. Для спеціалізованих фігур, наприклад, паралелограмів, ця формула спрощується до P = 2(a+b).
Теорема Варіньона: Прихована Симетрія (Нетривіально)
Ця теорема, названа на честь французького математика П’єра Варіньона, розкриває елегантну приховану симетрію: чотирикутник, утворений послідовним сполученням середин сторін будь-якого чотирикутника (навіть неопуклого), завжди є паралелограмом.
Для глибшого розуміння: якщо ви прагнете не просто запам’ятати правила, а зрозуміти приховану логіку геометрії, курси математики для дітей від JustSmart допоможуть систематизувати ці знання та вивести їх на новий рівень.
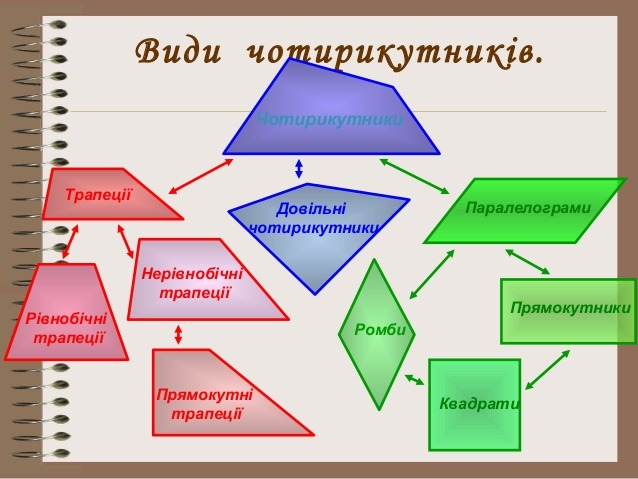
Класифікація чотирикутників
Усі чотирикутники можна поділити на дві великі групи: ті, що мають попарну паралельність сторін (Паралелограми), та незалежні фігури, які мають лише часткову симетрію.
Династія паралелограма
Паралелограм — це центральна фігура, у якої протилежні сторони попарно паралельні. Він має центральну симетрію.
- Ключова властивість: Діагоналі точкою перетину діляться навпіл.
Ромб і Прямокутник — це два напрямки розвитку властивостей паралелограма:
Квадрат — це єдиний правильний чотирикутник, який об’єднує всі властивості Ромба та Прямокутника, задовольняючи визначенню правильного багатокутника.
Незалежні Фігури: Трапеція та Дельтоїд
Ці фігури не належать до родини паралелограмів, але мають свої унікальні правила та симетрію.
- Трапеція (трапецоїд): Чотирикутник, у якого лише дві протилежні сторони паралельні (основи). Якщо бічні сторони рівні, це рівнобічна трапеція (її діагоналі рівні).
- Дельтоїд (або “Змій”): Чотирикутник, у якого дві пари сусідніх сторін рівні. Його ключова властивість — діагоналі перпендикулярні, а одна з діагоналей є віссю симетрії та бісектрисою кутів.
Знання властивостей усіх цих фігур (від трапеції до квадрата) є критично важливим. Якщо ви готуєтеся до важливих іспитів, де потрібне глибоке знання цих взаємозв’язків та теорем, рекомендуємо курси підготовки до НМТ, щоб перетворити розрізнені знання на системну картину.
Обчислення площі чотирикутника
Обчислення площі чотирикутника (S) є ключовою прикладною навичкою. Для різних типів фігур застосовуються спеціальні або універсальні формули. Для будь-якого опуклого чотирикутника (навіть нерегулярного) площа може бути знайдена, якщо відомі довжини діагоналей та синус кута між ними:
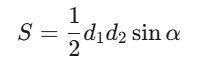
Ця формула є особливо зручною для фігур з перпендикулярними діагоналями (Ромб, Дельтоїд, Квадрат), де sin 90 градусів = 1, що спрощує формулу.
Знання цих формул перевіряється на практиці. Щоб навчитися швидко застосовувати формули на час іспиту, спробуйте пройти тести НМТ з математики та перевірте свій рівень готовності.
Вписані та описані чотирикутники
Вписаний чотирикутник (циклічний) — це фігура, всі вершини якої лежать на одному колі. Основна умова, що визначає таку фігуру, пов’язана з кутами: суми його протилежних кутів дорівнюють 180 градусів.
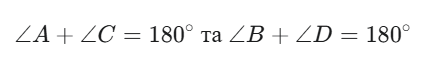
Описаний чотирикутник (тангенціальний) — це фігура, у яку можна вписати коло, що дотикається до всіх його сторін . Ця властивість регулюється Теоремою Піто: суми його протилежних сторін мають бути рівні.
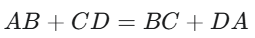
Освоєння умов вписані та описані чотирикутники є обов’язковим для розв’язання завдань підвищеної складності. Поглибити ці знання допоможуть курси математики для дітей.
Висновок
Чотирикутники є однією з найбільш фундаментальних і водночас багатогранних геометричних фігур. Їхнє вивчення виходить далеко за межі шкільного матеріалу, охоплюючи принципи стійкості (у будівництві), гнучкості (в інженерії) та симетрії (у математиці).
Ми розглянули династію Паралелограма, унікальні фігури (Трапеція, Дельтоїд), універсальні формули площі та елегантні теореми циклічних та тангенціальних чотирикутників. Освоєння цієї теми — це ключ до успіху в геометрії, що дозволяє не лише розв’язувати задачі, а й бачити логіку у світі, що нас оточує.
